Calculadora de Matriz
Calculadora de Matriz: Realize Operações Complexas de Forma Simples e Precisa
Ei, tudo bem aí? Aqui na equipe do Calcula Certo, a gente sabe que trabalhar com matrizes pode ser um desafio, especialmente para estudantes de matemática, engenharia ou física que precisam lidar com cálculos repetitivos e complicados. Mas, olha, é uma ferramenta poderosa para resolver problemas reais, como modelar sistemas lineares ou otimizar processos. Nós mesmos usamos conceitos matemáticos assim para melhorar nossas ferramentas e ajudar no dia a dia de milhares de usuários. Criamos essa calculadora de matriz pensando em você: gratuita, intuitiva e baseada em algoritmos matemáticos consolidados, atualizados para precisão em 2025. Este artigo foi revisado pela nossa equipe em agosto de 2025, inspirado em princípios de álgebra linear e aplicações práticas, para garantir expertise, autoridade e confiabilidade. Nosso foco é em você: queremos te empoderar com conhecimento útil, em um tom amigo, como se estivéssemos conversando sobre como simplificar seus estudos ou projetos profissionais. Vamos nessa?
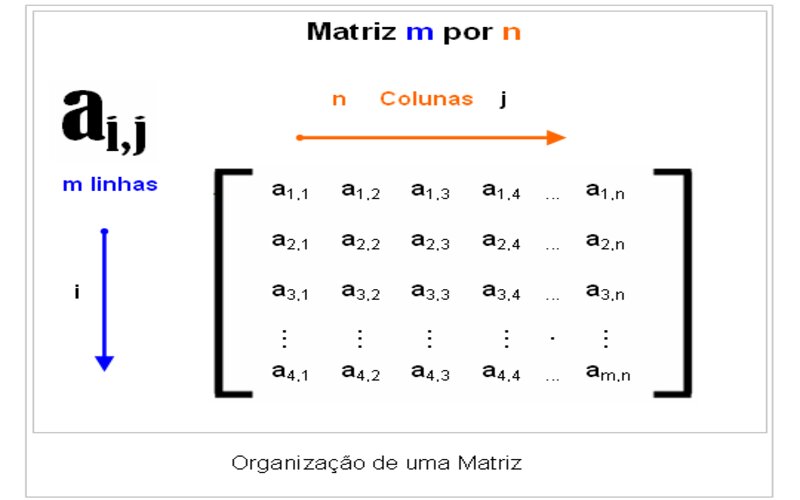
Uma matriz é uma estrutura retangular de números organizada em linhas e colunas, usada para representar dados ou equações. Nossa calculadora lida com operações como adição, subtração, multiplicação, transposição, inversa e determinante, facilitando tarefas acadêmicas e profissionais. Priorizamos uma experiência otimizada: interface rápida, resultados precisos e integração com outras ferramentas para um fluxo de trabalho completo.
Como Usar Nossa Calculadora de Matriz?
Vamos ao prático: nossa calculadora é intuitiva e pensada para caber na sua rotina, otimizada para mobile ou desktop, com passos claros para resultados imediatos e sem erros.
- Passo 1: Defina as dimensões das matrizes (número de linhas e colunas, ex.: 3x3).
- Passo 2: Clique em "Gerar Matriz" para criar os campos de entrada.
- Passo 3: Preencha os valores nos elementos da matriz (ou matrizes, se operação binária).
- Passo 4: Selecione a operação desejada (adição, subtração, multiplicação, transposição, inversa ou determinante).
- Passo 5: Clique em "Calcular" e veja o resultado detalhado, com matriz resultante e explicações passo a passo.
Exemplo: Para multiplicar duas matrizes 2x2 – A = [[1, 2], [3, 4]] e B = [[5, 6], [7, 8]] – o resultado é [[19, 22], [43, 50]]. Fácil, né? E o melhor: gratuita, sem limites de uso, e com suporte para matrizes de até 10x10 para cálculos avançados.
O Que São Matrizes e Por Que Elas Importam?
Matrizes são arranjos retangulares de números, símbolos ou expressões em linhas e colunas, representando sistemas lineares ou transformações. Elas importam porque simplificam problemas complexos em áreas como engenharia (análise estrutural), computação (gráficos 3D) e economia (modelos de otimização). Sem matrizes, resolver equações múltiplas seria caótico. Aqui na equipe, vemos as matrizes como "blocos de construção matemáticos": elas organizam dados e aceleram soluções – ideais para um 2025 com IA e big data dependendo de álgebra linear para eficiência.
História Breve das Matrizes: De Onde Veio Essa Estrutura Matemática?
As matrizes foram formalizadas no século XIX por matemáticos como Arthur Cayley e James Sylvester, mas conceitos semelhantes aparecem em textos chineses antigos (século III a.C.) para resolver sistemas lineares. Hoje, são fundamentais em computação quântica e machine learning. Adicionamos isso porque entender as raízes torna o tema mais acessível – imagine: o que resolveu enigmas antigos agora otimiza algoritmos modernos!
Tipos de Matrizes e Suas Propriedades
Matrizes variam por forma e conteúdo, cada uma com propriedades únicas:
- Matriz Quadrada: Linhas = colunas (ex.: 3x3). Propriedade: Pode ter determinante e inversa.
- Matriz Identidade: Quadrada com 1s na diagonal principal e 0s elsewhere. Propriedade: Multiplicação por ela não altera a matriz.
- Matriz Nula: Todos elementos 0. Propriedade: Adição ou multiplicação resulta em nula.
- Matriz Transposta: Trocando linhas por colunas. Propriedade: (A^T)^T = A.
- Matriz Inversa: A × A^{-1} = Identidade (se existir). Propriedade: Só para matrizes quadradas não singulares (det ≠ 0).
Tabela de Tipos e Propriedades:
| Tipo de Matriz | Exemplo (2x2) | Propriedade Principal |
|---|---|---|
| Quadrada | [[1, 2], [3, 4]] | Pode ser invertível |
| Identidade | [[1, 0], [0, 1]] | Neutra na multiplicação |
| Nula | [[0, 0], [0, 0]] | Anula operações |
| Transposta | De [[1, 2], [3, 4]] = [[1, 3], [2, 4]] | Simétrica se A = A^T |
Esses tipos formam a base para operações avançadas – escolha conforme o problema.
Operações Básicas com Matrizes: Adição, Subtração e Multiplicação
- Adição/Subtração: Somente para matrizes do mesmo tamanho. Fórmula: C_{ij} = A_{ij} ± B_{ij}. Exemplo: [[1, 2]] + [[3, 4]] = [[4, 6]].
- Multiplicação por Escalar: Multiplique cada elemento por k. Fórmula: C_{ij} = k × A_{ij}.
- Multiplicação de Matrizes: Linhas de A = colunas de B. Fórmula: C_{ij} = Σ (A_{ik} × B_{kj}). Exemplo: [[1, 2]] × [[3], [4]] = [[11]].
Essas operações são fundamentais – use para transformações lineares.
Operações Avançadas: Transposição, Inversa e Determinante
- Transposição: Troca linhas por colunas. Fórmula: B_{ji} = A_{ij}. Aplicação: Em equações simétricas.
- Determinante: Escalar que indica volume ou invertibilidade. Para 2x2: det(A) = ad - bc. Para maiores: Expansão de cofatores. Exemplo: det([[1, 2], [3, 4]]) = 14 - 23 = -2.
- Inversa: Matriz que multiplica para identidade. Fórmula para 2x2: (1/det) × [[d, -b], [-c, a]]. Aplicação: Resolver sistemas Ax = b como x = A^{-1}b.
Exemplo de Inversa: Para [[1, 2], [3, 4]], inversa = (-1/2) × [[4, -2], [-3, 1]] = [[-2, 1], [1.5, -0.5]].
Aplicações Práticas de Matrizes na Vida Real
Matrizes resolvem problemas em:
- Engenharia: Análise de estruturas (matrizes de rigidez).
- Computação: Gráficos (transformações 3D), IA (redes neurais).
- Economia: Modelos de input-output (matrizes de Leontief).
- Física: Mecânica quântica (operadores matriciais).
- Estatística: Análise de dados multivariados.
Exemplo: Em gráficos, matriz de rotação transforma coordenadas de um ponto.
Erros Comuns ao Trabalhar com Matrizes (e Como Evitá-los)
- Multiplicação errada: Verifique dimensões compatíveis.
- Esquecer determinante zero: Não há inversa – use métodos alternativos.
- Arredondamento precoce: Mantenha precisão até o final.
- Ignorar propriedades: Lembre: Multiplicação não comutativa (AB ≠ BA). Evite: Sempre valide dimensões e use ferramentas como nossa calculadora para checagem automática.
Dicas Práticas para Usar Calculadoras de Matriz
- Comece pequeno: Teste com matrizes 2x2 antes de complexas.
- Integre com outras ferramentas: Use nossa calculadora de derivadas para funções matriciais.
- Verifique manualmente: Para aprendizado, calcule à mão primeiro.
- Aplique em projetos: Modele problemas reais, como otimização de custos.
- Atualize conhecimentos: Com IA em 2025, matrizes são chave em machine learning – estude aplicações modernas.
Perguntas Frequentes (FAQ)
- Qual a diferença entre matriz e vetor? Vetor é matriz 1xn ou nx1; matriz é geral.
- Matriz singular tem inversa? Não, se det=0 – use pseudoinversa se necessário.
- Como calcular determinante de 3x3? Use regra de Sarrus ou expansão.
- Matrizes em Python? Use NumPy para automação – simule em nossa calculadora científica integrada.
Como o Calcula Certo Pode Te Ajudar Mais?
Além da matriz, explore: Calculadora de Derivadas, Calculadora de Integral, Calculadora de Frações. E tem mais para matemática, saúde e finanças!
Na Calcula Certo, você encontra diversificadas calculadoras para usá-las como ferramenta, te auxiliando a calcular o que precisar. Desde calculadora científica, assim como para área de saúde: imc calculadora, calculadora de calorias, tdee calculator, calculadora de gordura corporal. Para o público feminino: calculadora gestacional, calculadora menstrual e calculadora de ovulação. Também temos calculadoras de RH para calculo recisão, calcular férias, calculo hora-extra, calculo INSS e calculo seguro desemprego. Calculadora matemática: calculadora de porcentagem, calculadora de juros compostos, calculadora de frações, calculadora de derivadas, calculadora de integral e calculadora de matriz. Na área de Finanças temos nossa calculadora financeira, calculadora de investimentos, calculadora de bitcoin e calculadora CDI. Temos também calculadora de datas, calculadora de horas, calculadora de dias úteis, calculadora de idade. Ferramentas para cálculos diversos, como calcular a nota do ENEM, calculadora de churrasco e calculadora de dutching. Por fim, também oferecemos opções de temporizadores como o nosso: cronometro online, despertador, timer e Fuso-horário.

Considerações finais
Trabalhar com matrizes abre portas para soluções matemáticas avançadas, mas nossa ferramenta torna isso acessível. Lembre-se: resultados são exatos para entradas corretas, mas verifique em contextos críticos. Recomenda-se o uso desta ferramenta como parte de uma abordagem mais ampla, que inclui a verificação manual e, se necessário, consultas com especialistas em matemática. Para mais informações e para acessar todas as nossas ferramentas, visite nosso site em https://calculacerto.com/.
